glucopy.plot.fourier#

glucopy.plot.fourier(gf: ~glucopy.classes.Gframe.Gframe, n: int = 10, amplitude_guess: [<class 'float'>] = None, phase_guess: [<class 'float'>] = None, num_days: int = 0, full_output: bool = False, height: float = None, width: float = None)[source]#

Plots the best-fit curve obtained by a Fourier series using scipy.optimize.curve_fit. The Fourier series is given by:

\[f(t) = m + \sum_{i=1}^{N} A_i \cos(\frac{2\pi i (t-PHS_i)}{hourRange})\]

where:

\(m\) is \(\frac{AUC(h)}{hourRange}\).
\(AUC\) is the area under the curve.
\(A_i\) is the amplitude of the \(i\)-th harmonic.
\(PHS_i\) is the phase shift of the \(i\)-th harmonic.

Parameters:

gf (Gframe) – Gframe object to plot
n (int, default 10) – (\(N\)) Number of harmonics to fit
amplitude_guess ([float], default None) – Initial guess for the amplitudes, if None, all amplitudes are set to 1
phase_guess ([float], default None) – Initial guess for the phase shifts, if None, all phase shifts are set to 1
num_days (int, default 0) – Number of days to plot, if 0 all days are plotted.
full_output (bool, default False) – If True, returns the figure and the best-fit parameters
height (float, default None) – Height of the figure
width (float, default None) – Width of the figure

Returns:

fig – Figure object

Return type:

plotly.graph_objects.Figure

Examples

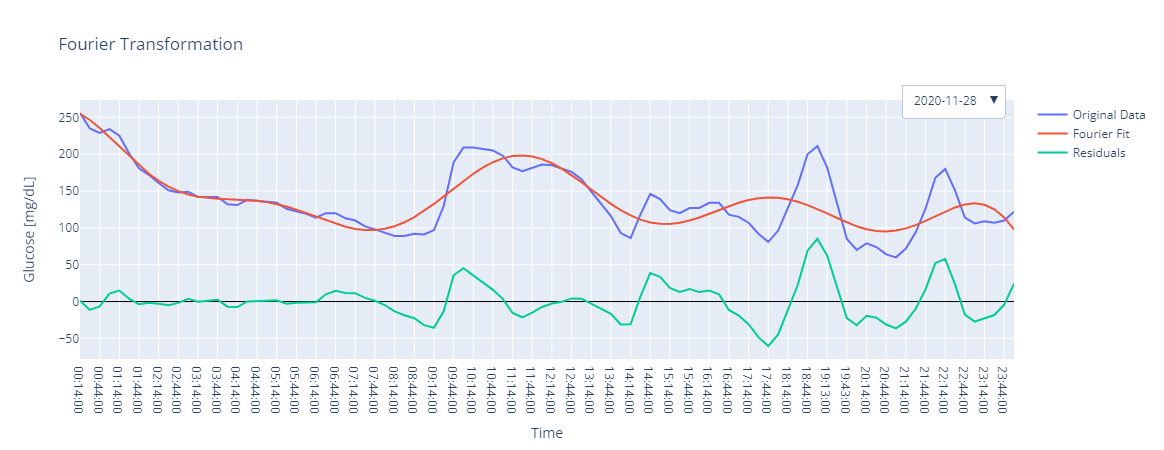
Plot the Fourier Transformation with 5 harmonics for the first 5 days.

In [1]: import glucopy as gp

In [2]: gf = gp.data()

In [3]: gp.plot.fourier(gf, n=5, num_days=5)
Error fitting day 2020-11-27: The number of func parameters=12 must not exceed the number of data points=11
Out[3]: 

Plot the Fourier Transformation with 10 harmonics for the first 5 days.

In [4]: fig = gp.plot.fourier(gf, n=10, num_days=5)
Error fitting day 2020-11-27: The number of func parameters=22 must not exceed the number of data points=11

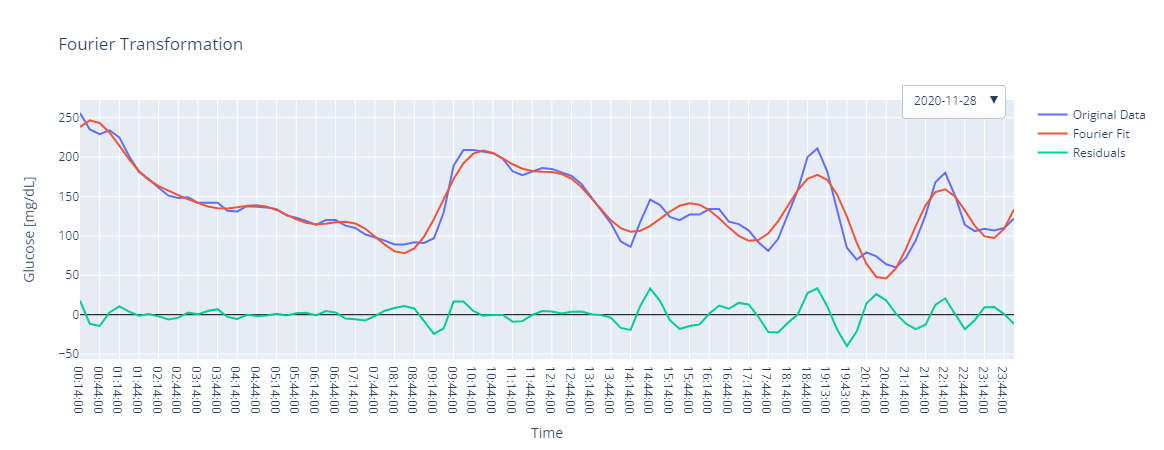
Note that in both cases, the day 2020-11-27 fails to fit, that is because the number of glucose values is too low to fit the Fourier series. To solve this issue, we can decrease the number of harmonics, but this will decrease the quality of the fit for the rest of the days.